| |
| 7.1 |
Inequalities |
| |
| Definition |
|
The relationship between two quantities that do not have the same value.
|
|
| |
| Symbol |
Meaning |
| \(\gt\) |
Greater than |
| \(\lt\) |
Less than |
|
| |
| Example |
|
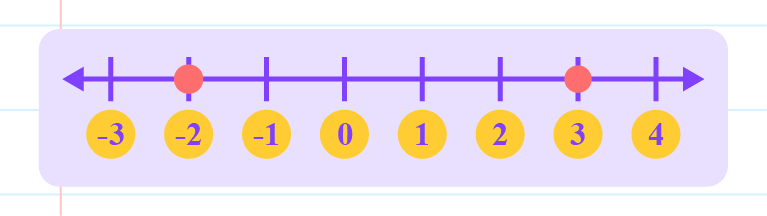
|
|
From the number line above, \(–2\) lies to the left of \(3\).
So, \(–2\) is less than \(3\).
Thus, the inequality is \(–2 < 3\).
|
|
| |
| Example |
|
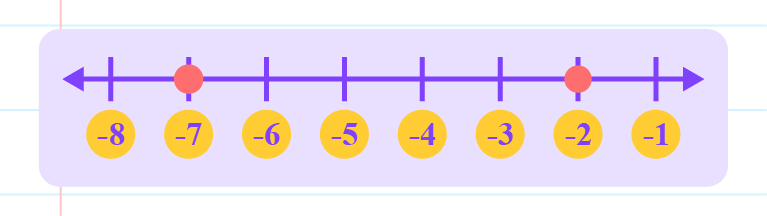
|
|
From the number line above, \(–2\) lies to the right of \(-7\).
So, \(–2\) is greater than \(-7\).
Thus, the inequality is \(–2 > -7\).
|
|
| |
| Describe inequality and form algebraic inequality: |
| |
| Example |
|

|
|
From the number line above, \(x\) is less than \(8\).
Thus, \(x\lt 8\).
|
|
| |
| Identify relationship: |
| |
| Symbol |
Meaning |
| \(\geq\) |
Greater than or equal to |
| \(\leq\) |
Less than or equal to |
|
| |
| Properties of inequalities: |
| |
|
Converse property of inequality
|
| |
| Example |
|
State the converse property of inequality of \(-23\gt-32\).
|
|
Answer: \(-32\lt-23\)
|
|
| |
|
Transitive property of inequality
|
| |
| Example |
|
State the transitive property of inequality of \(-15\lt-8\lt0\).
|
|
Answer: \(-15\lt0\)
|
|
| |
- The inequality symbol remains unchanged when adding or subtracting a positive or negative number to or from both sides of the inequality.
|
| |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a+c&\lt b+c.\\\\ \end{aligned}\) |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a-c&\lt b-c. \\\\\end{aligned}\) |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a+(-c)&\lt b+(-c).\\\\ \end{aligned}\) |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a-(-c)&\lt b-(-c).\end{aligned}\) |
|
| |
- The inequality symbol remains unchanged when multiplying or dividing both sides of the inequality by a positive number.
|
| |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a\times c&\lt b\times c.\\\\ \end{aligned}\) |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,\dfrac{a}{c}&\lt \dfrac{b}{c}.\end{aligned}\) |
|
| |
- The direction of the inequality symbol is reversed when multiplying or dividing both sides of the inequality by a negative number.
|
| |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,a\times (-c)&\gt b\times (-c).\\\\ \end{aligned}\) |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,\dfrac{a}{-c}&\gt \dfrac{b}{-c}.\end{aligned}\) |
|
| |
|
Additive inverse
- When both sides of the inequality are multiplied by \(-1\), the direction of the inequality symbol is reversed.
|
| |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,-a&\gt -b.\end{aligned}\) |
|
| |
|
Multiplicative inverse
- When performing reciprocal of both numbers on both sides of the inequality, the direction of the inequality symbol is reversed.
|
| |
| \(\begin{aligned} \text{If }\,a&\lt b, \\\\\text{then }\,\dfrac{1}{a}&\gt \dfrac{1}{b}.\end{aligned}\) |
|
| |